Suite à l’article où je décrivais les grands nombres à travers les tableaux, voilà pour tous ceux qui sont obligés d’utiliser les listes, les fonctions correspondantes.

La grande différence avec les tableaux, est que les tableaux se traitent de manière linéaire, alors que les listes se traitent de manière récursive.

Qu’est-ce que la récursivité ? C’est la propriété qu’a une fonction de s’auto-appeler, c’est à dire de se rappeler elle-même plusieurs fois. On décrit ça en disant que l’on ouvre plusieurs feuilles de calcul en simultané.

Pratiquement, une fonction qui se rappelle stocke sur la pile ses données, et son point de retour à la fin de la fonction appelée sur le stack, et quand la sous-routine se termine, les paramètres de la précédente ( appelée mère ), sont restaurés.

Théoriquement, il y a deux types de récursivité, la récursivité terminale, et la récursivité non-terminale.

La récursivité non-terminale, c’est quand on rappelle la fonction avec les nouveaux paramètres, et qui se termine en renvoyant le résultat, c’est à dire que le résultat va remonter toutes les feuilles de calcul.

Pour la récursivité terminale, on rappelle la fonction en lui passant un accumulateur, c’est lui qui contiendra le retour, et évitera ainsi de tout désempiler lors du retour.

Les deux méthodes sont équivalentes en temps machine, mais il faut les connaître, c’est très utile suivant le type de calcul à effectuer.

C’est un ensemble de cases qui se suivent, auxquelles on accède par la première, puis la suivante, et ainsi de suite jusqu’à la dernière.

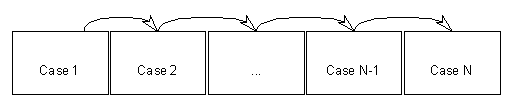
Une cellule de la liste contient l’adresse de la suivante, c’est pour cela que l’on les appelle les listes chaînées.

Un exemple, en prenant pour convention le stockage à l’envers du nombre dans la liste, c’est à dire que le premier sera l’unité puissance zéro, on aura, pour 51987 :

La liste correspondant pointera sur le 7, plus facile à utiliser pour additionner deux listes, mais on peut choisir un autre sens.

L’avantage des listes étant que, à chaque fois que l’on a besoin d’une nouvelle case, on la crée. Voyons la déclaration d’une liste :

Type

Liste = ^Cellule;

Cellule = Record

Caract : Char;

Suivant : Liste;

End;

Il s’agit d’un pointeur sur un type record, contenant le caractère, ou un byte, suivant son goût personnel, et l’affichage. Ensuite, il faut des instructions pour initialiser une liste :

Function Init : Liste;

Begin

Init := Nil

end;

Et d’autres pour créer le premier élément. On procédera ainsi:

var A : liste;

begin

a := Init;

end;

Function Cons (Element : Char; L : Liste) : Liste;

Var

Nouv_Liste : Liste;

Begin

New(Nouv_Liste); (* on crée la cellule *)

Nouv_Liste^.Caract := Element; (* on met le caractère *)

Nouv_Liste^.Suivant := L; (* on prend l'adresse envoyée comme *)

Cons:=Nouv_Liste; (* nouvelle case vide potentielle*)

(* et on rattache le tout *);

End;

Bien évidemment, on ne peut rajouter une case qu’en tête de liste, d’où le besoin d’établir des conventions, comme stoker le nombre à l’envers, et la première case lue sera celle des unités puissance 0.

Une autre fonction nécessaire est savoir si la liste est vide, si c’est le cas, il n’y a rien à traiter :

Function Liste_Est_Vide(L : Liste) : Boolean;

Begin

Liste_Est_Vide := (L=Nil)

End;

Maintenant, pour extraire un nombre, on ne peut extraire que la queue, je m’explique, la tête de la liste pointe sur NIL, au cas où on voudrait rajouter une case, et donc, comme le montre le graphe, c’est la queue de la liste qui contient l’adresse de la cellule suivante et ainsi de suite jusqu’à la tête.

Pour parcourir la liste, on lira la queue, puis on passera à la case suivante ... Il n’y a pas de parcours en sens inverse possible, car on ne garde pas trace de la cellule précédente, ce qui est d’ailleurs inutile dans le travail sur les nombres par les listes.

Voici donc comment lire la queue de la liste :

Function Premier (L : Liste) : Char;

Begin

Premier := L^.Caract

End;

Et comment la retirer pour lire la case suivante :

Function Reste (L : Liste) : Liste;

Begin

Reste := L^.Suivant

End;

Maintenant, pour admirer vos essais, voici comment afficher une liste :

Procedure Affiche_Liste(L : Liste);

Begin

If Not (Liste_Est_Vide(L)) Then

Begin

Write (Premier(L));

Affiche_Liste(Reste(L))

End

End;

Il arrive qu’au bout d’un moment on veuille savoir le nombre d’éléments d’une liste, voici comment y arriver :

Function Longueur (L:Liste):integer;

Var

TAILLE : Integer;

Begin

TAILLE := 0;

Repeat

L := Reste(L);

TAILLE := TAILLE + 1;

Until Liste_est_vide (L);

LONGUEUR := TAILLE;

End;

Et à cause de la convention de stockage, il arrive parfois que, par la récursivité, que la liste soit renvoyée à l’envers, et donc il faut l’inverser :

Function Miroir (L: liste) : Liste;

Var

L_inv : Liste;

Begin

L_inv:=init;

While not (Liste_est_vide(L)) do

Begin

L_inv:=cons(premier(L),L_inv);

L:=reste (L);

End;

Miroir:=L_inv;

End;

Le renversement à été fait de manière linéaire, et ne pouvait pas être fait de manière récursive ici à cause des listes. Voyons maintenant comment comparer deux listes, ci-dessous ce test, on envoie A et B et on veut la comparaison :

Function Test_A_Plus_Grand_Que_B (NA,NB: Liste): Integer;

Var

B: Integer;

(* NB : Valeurs possibles de B:

0: Egalité de NA et NB

1: NA>NB

2: NA<NB *)

Begin

If Longueur(NA)>Longueur(NB) then

B:=1

Else

If Longueur(NA)<Longueur(NB) then

B:=2

Else If Longueur(NA)=Longueur(NB) Then

Begin

NA:=Miroir(NA);

NB:=Miroir(NB);

While (premier(NA)=premier(NB))

and (not Liste_est_vide(NA)) do

Begin

NA:=Reste(NA);

NB:=Reste(NB);

End;

If (Liste_est_vide(NA) and Liste_est_vide(NB)) then

B:=0

Else

If ( ord (premier(NA)) )> ( ord(premier(NB))) then

B:=1

Else

If ( ord (premier(NA)) ) <

( ord(premier(NB)) ) then

B:=2

End;

Test_A_plus_grand_que_B:=B;

End;

Plus compliqué qu’avec les tableaux, et plus lent oui, mais les inconvénients ont desfois des avantages. Ci-après, une fonction qui extrait p éléments de la liste N , ça peut servir desfois :

Function XTRACT (N:Liste; P: Integer) : Liste;

Var

RES: Liste;

Begin

RES:=Init;

N:=Miroir(N);

While (not(Liste_est_vide(N)) and (P>0)) do

Begin

RES:=Cons(Premier(N),RES);

N:=Reste(N);

P:=P-1;

End;

XTRACT:=RES;

End;

Function Addition (NA,NB:liste):liste;

Var

NC : Liste;

retenue: Integer;

a,b : Integer;

Procedure fin_d_add(var ND:liste);

Begin

While not (liste_est_vide(ND)) do

Begin

NC:=cons(chr( ((ord(premier(ND))+retenue-zero) mod 10)+zero),NC);

retenue:=(ord(premier(ND))+retenue-zero) div 10;

ND:=reste(ND);

End

End;

Begin

If Liste_est_vide(NA) then NA:=cons('0',NA);

If Liste_est_vide(NB) then NB:=cons('0',NB);

NC:=init;

retenue:=0;

While not ((Liste_est_vide(NA)) and (Liste_est_vide(NB))) do

If ((Liste_est_vide(NA)) and (not(Liste_est_vide(NB)))) then

fin_d_add(NB)

Else If ((Liste_est_vide(NB)) and (not(Liste_est_vide(NA)))) then

fin_d_add(NA)

Else

Begin

A:=ord(premier(NA))-zero;

B:=ord(premier(NB))-zero;

NC:=cons( chr( ( (a+b+retenue) mod 10)+zero) , NC);

retenue:=( (a+b+retenue) div 10 );

NA:=reste(NA);

NB:=reste(NB);

End;

If retenue<>0 then

NC:=cons(chr(retenue+zero),NC);

Addition:=Miroir(NC);

End;

Function SOUSTRACTION (NA,NB: liste) : liste;

Function SOUSTRACT (NA,NB:liste) : liste;

Var

NC: Liste;

Retenue : Integer;

a,b,ret : Integer;

(************** Fin de la soustraction quand liste vide *************)

Procedure FIN_D_SOUS(Var ND: liste);

Var

C: Integer;

Begin

While not (liste_est_vide(ND)) do

Begin

RET:=0;

C:=ord(premier(ND))-zero;

if C<retenue then

Begin

C:=C+10;

Ret:=1;

End;

NC:=cons(chr(c-retenue+zero),NC);

retenue:=ret;

ND:=reste(ND);

End

End;

(* Fin de FIN_D_SOUS *)

(* début de SOUSTRACT *)

Begin

NC:=Init;

Retenue:=0;

A:=0;

B:=0;

While not ((liste_est_vide(NA)) and (liste_est_vide(NB))) do

if liste_est_vide(NB) then

FIN_D_SOUS(NA)

else

Begin

A:=ord(premier(NA))-zero;

B:=ord(premier(NB))-zero;

ret:=0;

If A<(B+retenue) then

Begin

A:=A+10;

RET:=1;

End;

NC:=cons(chr(a-(b+retenue)+zero),NC);

retenue:=ret;

NA:=Reste(NA);

NB:=Reste(NB);

End;

Soustract:=Miroir(NC);

End;

(* Fin de SOUSTRACT *)

Var

T: Integer;

Begin

T:=Test_A_Plus_Grand_Que_B(NA,NB);

If T=0 then

Soustraction:=cons('0',nil)

Else If T=1 then

Soustraction:=Soustract(NA,NB)

Else If T=2 then

Soustraction:=Soustract(NB,NA);

End;

Puisque nous voilà lancés, maintenant voyons la multiplication d’une liste par une constante, chose fort peu aisée, et on remarque ici un retournement du résultat de l’opération :

Function MultC (L1:Liste; d: integer):Liste;

Var

Multiplic: Liste;

Retenue: Integer;

Begin

If (d<>0) then

Begin

Multiplic:=init;

Retenue:=0;

While not (Liste_est_vide(L1)) do

Begin

Multiplic:=cons( chr((((ord(premier(L1zero)*d+retenue) mod 10)+zero),Multiplic);

Retenue:=((Ord(premier(L1))-zero)*d+Retenue) div 10;

L1:=Reste(L1);

End;

If (Retenue<>0) then

Multiplic:=cons( chr (retenue+zero), multiplic);

MultC:=Miroir(Multiplic);

End

Else MultC:=cons('0',Nil);

End;

Function Multiplication (N1,N2: Liste) : Liste;

Function Multiplicat (L1,L2: Liste): Liste;

Var

L_totale : Liste;

L_partielle : Liste;

I : Integer;

N : Integer;

Puiss : Integer;

Begin

L_Totale:=Init;

L_partielle:=Init;

Puiss:=1;

For I:=1 to Longueur (L2) do

Begin

L_partielle:=(MultC(L1,( ord(premier(L2))) - zero));

For N:=1 to (Puiss-1) do

Begin

L_partielle:=Cons('0',L_partielle);

End;

Puiss:=Puiss+1;

L_totale:=Addition(L_totale,L_partielle);

L2:=Reste(L2);

End;

Multiplicat:=L_Totale;

End;

Begin

If longueur(N1)<Longueur(N2) then

Multiplication:=Multiplicat(N2,N1)

Else Multiplication:=Multiplicat(N1,N2);

End;

Ici plus bêtement, on multiplie p fois N par 10 pour le mettre à la puissance p voulue :

Function PUISS_10 (N:Liste; NB_ZEROS: Integer) : Liste;

Var

I: Integer;

Begin

For I:=NB_Zeros Downto 0 do

N:=Multiplication (N,Cons('1',Cons('0',nil)));

Puiss_10:=N;

End;

Ca c’était le digestif avant le second plat de résistance : la division. Essayez donc de comprendre tout seul, la mise en page me faire damner...

Function DIVISION (NA,NB:liste; Var RESTE: Liste):liste;

Function Divis (N1,N2: Liste; RESULT : Liste; Var RESTE: Liste) : Liste;

Begin

If TEST_A_PLUS_GRAND_QUE_B (Xtract(N1,LONGUEUR(N2)),N2)=2 then

If TEST_A_PLUS_GRAND_QUE_B (Xtract(N1,LONGUEUR(N2)+1),N2)=2 then

Begin

Divis:=Miroir(Result);

Reste:=N1;

End

Else Divis:=Divis(

Soustraction(N1,

Puiss_10(N2,

Longueur(N1)-Longueur(N2)-1

)

),

N2,

Miroir(Addition(miroir(Result),Cons('1',nil))),

reste)

Else

Divis:=Divis (Soustraction(N1,

Puiss_10(N2,

Longueur(N1)-Longueur(N2))

), N2,

Miroir(Addition(Miroir(Result),Cons('1',nil))),

reste)

End;

Begin

If TEST_A_PLUS_GRAND_QUE_B(NA,NB)=1

Then Division:=Divis(NA,NB,nil,reste)

Else If TEST_A_PLUS_GRAND_QUE_B(NA,NB)=2

Then Division:=Divis(NB,NA,nil,reste)

Else Division:=nil

End;

Vous venez d’admirer un grand moment de récurrence de listes, de rappels de fonctions. Ca serait vraiment très long à schématiser pour vous expliquer, mais je garde un grand espoir de vous faire un jour un cours de numération.

Et pour finir, le modulo de A par B, du gâteau :

Function MODULO(NA,NB:Liste):Liste;

Var

DIVI,RESTE:Liste;

Begin

Divi:=init;

Reste:=init;

Divi:=Division(NA,NB,RESTE);

Modulo:=reste;

End;

Pour aller plus loin ... je signale qu’il existe une fonction pré-existante en C utilisable par LIST.H, et qui dans le même genre définit des arbres binaires... Si cela vous intéresse, je vous en parlerai. Sachez seulement qu’un arbre binaire est une cellule qui pointe sur deux autres cellules et ainsi de suite, ce qui en le représentant sur du papier donne une sorte d’arbre.

Autre chose, si vous faites un travail à bases de suites de Fibonnacci, contactez moi, j’ai un rapport de 40 pages au moins et des programmes à ce sujet.

Famous last words : Bien sûr, si certains bouts de programmes ne marchent pas, où si vous avez mieux, je suis prêt à tout accueillir pour améliorer ce document.