



Next: Relations Client / Serveur
Up: Architecture du Système d'Information
Previous: Agents dans un système
Table des matières
Index
Déplacer les données avec les agents est un phénomène coûteux à prendre en compte. Les machines sont un support fini, et leurs capacités ne sont donc pas infinies, en ce qui concerne le stockage et le transport de données. Quelques règles simples ([42]) peuvent être prises en compte concernant ces déplacements:
Pour un environnement de serveurs appelés par la suite 'SERVERS', connectés entre eux par un réseau. Les données contenues sur chaque serveur sont représentée par des grappes d'informations (Data Sets DS). On peut représenter l'usage qui est fait des données par
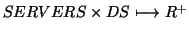 .
C'est une fonction qui associe à chaque serveur et grappe de données, le nombre de documents de cette grappe de de données qui seront demandés par des clients dans la zone géographique de ce serveur, pendant une période de temps donnée (semaine, mois...). De plus
.
C'est une fonction qui associe à chaque serveur et grappe de données, le nombre de documents de cette grappe de de données qui seront demandés par des clients dans la zone géographique de ce serveur, pendant une période de temps donnée (semaine, mois...). De plus 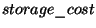 représente le coût pour stoquer localement une unité de données pour une période de temps, et la fonction
représente le coût pour stoquer localement une unité de données pour une période de temps, et la fonction 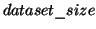 spécifie la taille de chaque ensemble de données en unité de données.
spécifie la taille de chaque ensemble de données en unité de données. 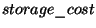 et
et 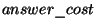 sont communs à tous les serveurs.
sont communs à tous les serveurs.
Définition: Le profit que le serveur s s'attend à obtenir en stoquant la grappe de données ds localement pour une période te temps donnée est:
Définition: Le profit que le serveur s s'attend à obtenir d'une grappe d'information ds située à la position loc du temps 0 à N, connaissant Vs est:
où r est le taux d'intérêt, et N est le nombre de périodes durant lequel l'environnement existe. Si l'environnement est considéré existant indéfiniment, alors 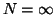 .
Dans ce cas:
.
Dans ce cas:
A partir de là, on peut utiliser cette fonction de coût pour savoir si les agents doivent se déplacer, déplacer l'information, ou s'il vaut mieux la laisser sur place.
Il s'ensuit un protocole de Commerce/Demande (Trading/Bidding), avec élection de la part du contracteur (contractor):
Définition:
S'il y a plus d'un proposant (bidder), avec la même valeur maximale de
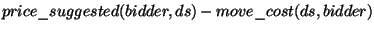 ,
alors le contracteur sélectionnera l'un d'eux (arbitrairement) pour être le gagnant (winner), et les autres seront considérés comme étant les proposants avec la seconde meilleure offre.
,
alors le contracteur sélectionnera l'un d'eux (arbitrairement) pour être le gagnant (winner), et les autres seront considérés comme étant les proposants avec la seconde meilleure offre.
D'autres applications de cette stratégie sont décrites dans [42].




Next: Relations Client / Serveur
Up: Architecture du Système d'Information
Previous: Agents dans un système
Table des matières
Index
epierre@e-nef.com
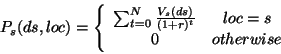
![]() ,
alors le contracteur sélectionnera l'un d'eux (arbitrairement) pour être le gagnant (winner), et les autres seront considérés comme étant les proposants avec la seconde meilleure offre.
,
alors le contracteur sélectionnera l'un d'eux (arbitrairement) pour être le gagnant (winner), et les autres seront considérés comme étant les proposants avec la seconde meilleure offre.
